edx 课程《Introduction to Probability - The Science of Uncertainty》Unit4 笔记
Unit 4: Discrete random variables
1. Probability mass functions and expectations (概率质量函数和期望)
1.1 随机变量的思想和定义
一切从一个例子出发
假设,现在有一个班,该班级有45个学生,我们想要知道每个学生的身高、体重以及体质指数。
每个学生都用编号 $1, 2, 3…, 45$ 表示。
所以,此时的样本空间 $\Omega = { 1, 2, 3 …, 45}$
接下来,对于一个编号为 $x$ 的学生来说,他有一个映射 $W$,可以让该学生从编号 $x$ 映射到另一个实数 $w$ (表示体重) ;同时还有另一个映射 $H$,可以让该学生从编号 $x$ 映射到另一个值实数 $h$ (表示身高)。
所以,现在我们可以知道 $W(x) = w$ 以及 $H(x) = h$
那么,这个 $W$ 和 $H$ 就是随机变量。
那么对于 体质指数 怎么表示呢?
因为体质指数 = 体重(kg)÷ 身高^2(m)
所以,我们有一个新的映射 $BMI$ 使得 $BMI(w, h) = bmi$
总结一下
从数学的角度理解,随机变量就是一个函数(映射),将样本空间 $\Omega$ 中的映射到另一个实数空间 $E$ 上。
根据上面这句话的理解,我们可以很形象地用数学公式表示随机变量
A random variable $X\colon \Omega \to E$ is a measurable function from a set of possible outcomes $\Omega$ to a measurable space $E$
另外,我们可以定义很多个随机变量,同时他们拥有相同的样本空间,就像例子中的身高和体重共享了同一个样本空间。
同时,随机变量的函数也是一个随机变量。比如,上面中的 体质指数 就是通过 身高、体重得到的。
1.2 PMF:Probability mass functions (概率质量函数)
数学公式上的定义:Suppose that $X: S → A (A {\displaystyle \subseteq R})$ is a discrete random variable defined on a sample space $S$. Then the probability mass function $f_X: A → [0, 1]$ for $X$ is defined as
$${\displaystyle f_{X}(x)=\Pr(X=x)=\Pr({s\in S:X(s)=x}).}$$
一个例子
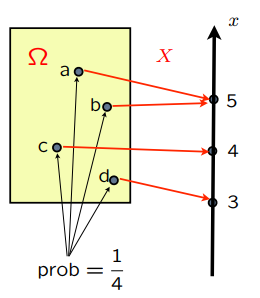
下图表示了一个概率质量函数。
有一个映射 $X$ 可以让 ${a ,b, c, d}$ 变成 ${ 3, 4, 5}$, 那么这个 $X$ 就是一个随机变量。现在我们想要求 $x = 5$ 的概率,就需要使用到概率质量函数。
通过计数可以知道 $P_X(5)=P(X=5)=1/2$, $P_X(4)=P(X=4)=1/4$, $P_X(3)=P(X=3)=1/4$, 所以这就是概率质量函数。
几个性质
- $p_X(x) \ge 0$
- $\sum_xp_X(x) = 1$
1.3 随机变量的例子
1.3.1 伯努利随机变量
定义:伯努利随机变量表示地是事件只有两种结果 1 和 0
伯努利随机变量的概率质量函数的数学形式为: $X={\begin{cases}1&{\text{if }}p,\[6pt]0&{\text{if }}1-p.\end{cases}}$
一般情况下,伯努利随机变量模拟地是一次实验的结果 (成功/失败) 或者(人头/数字)
还有一种指示器随机变量,它是伯努利随机变量的变种, $x=1$ 当且仅当 A 发生。
1.3.2 均匀随机变量
定义:符合数学公式 $P_X(x) = \frac{1}{b-a+1}$ 的都可以看作是均匀随机变量。
均匀随机变量有两个参数 $a, b$ 且 $a \leq b$
随机地选取 $a, a+1, …, b$ 概率都是相等的
样本空间为 ${ a, a+1, …, b}$
均匀随机变量模拟地是对于现有情况完全无知,为此,我们会认为任何事件发生的概率都是相等的。
1.3.3 二项随机变量
二项随机变量有两个参数,实验次数 $n$ 和硬币为 Heads 的概率 $p \in [0, 1]$
实验:对于 $n$ 次独立地投掷,一个硬币得到 Heads 的概率为 $P(Heads) = p$
样本空间:由 $H$ 和 $T$ 组成的序列合集,长度为 $n$
随机变量 $X$ 的含义是:Heads 被观察到的次数。
假设,现在$n=3$,那么 $P(H=0) = (_0^3)(1-p)^3$、$P(H=1) = (_1^3) p (1-p)^2$、$P(H=2) = (_2^3) p^2 (1-p)$、$P(H=3) = (_3^3) p^3$
二项随机变量模拟地是在$n$次独立实验中成功的次数
PMF 表示形式
$$P_X(k) = (_k^n) p^k (1-p)^{n-k}, for \ k = 0, 1, …, n$$
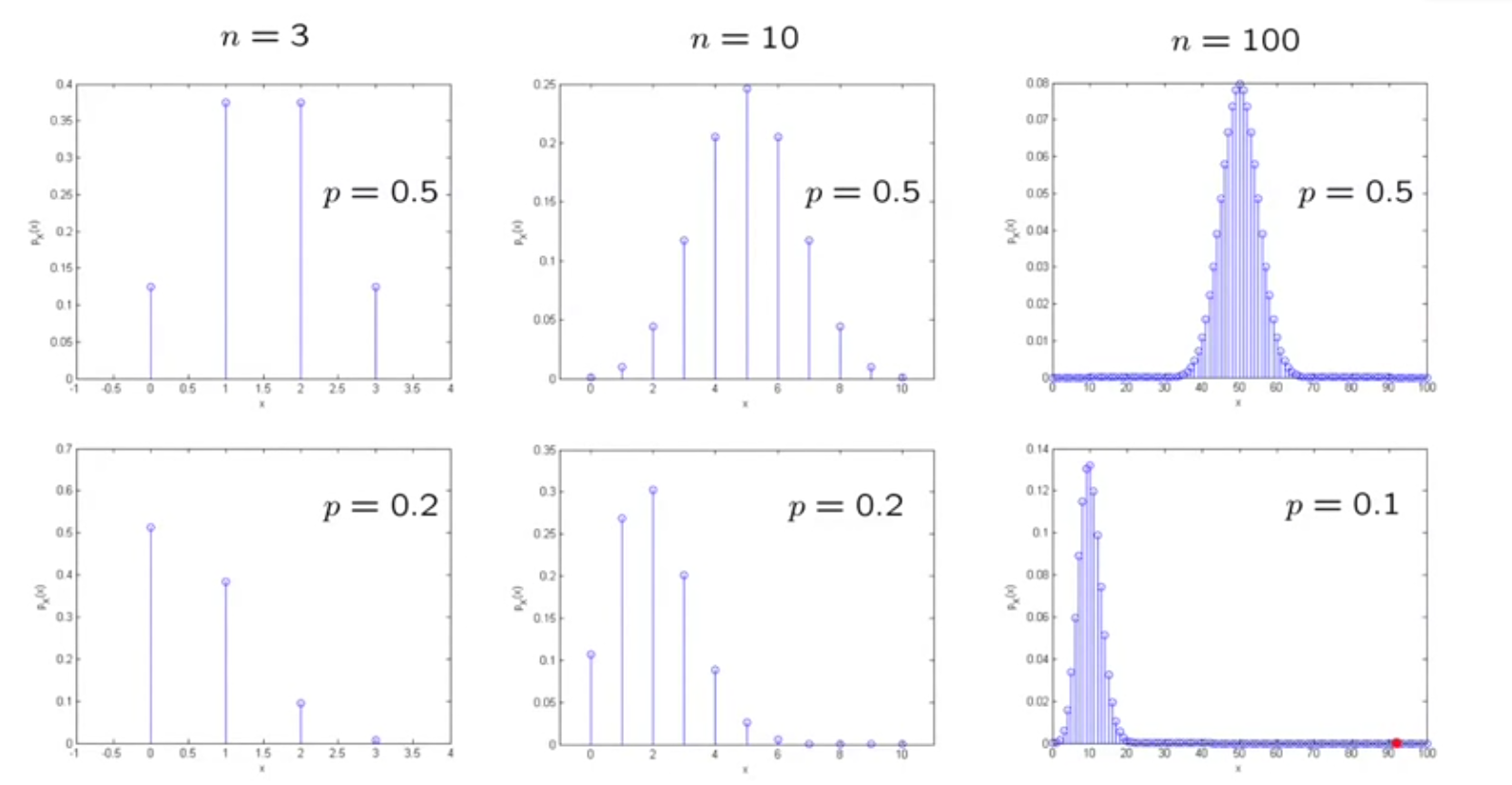
当实验次数足够多的时候,我们可以看出,根据二项分布的结果画出来的图非常接近正态分布
1.3.4 几何随机变量 (Geometric random variables)
一个参数,硬币为 Heads 的概率 $p \in [0, 1]$
实验:无穷多次的独立重复投掷一个硬币,且硬币为 Heads 的概率为 $P(Heads) = p$
样本空间:由 $H$ 和 $T$ 组成的序列合集,长度是无穷大小。
随机变量 $X$ 的含义是:直到第一出现 Heads 为止的投掷次数。
几何随机变量模拟地实验次数,直到成功为止,实验的次数
$$P_X(k) = P(X = k) = P(T, T, T, …, H) = (1-p)^{k-1} p$$
1.4 期望
期望:概率论中的核心地位。也被称为随机变量的均值。
假设 ${\displaystyle X}$ 是一个随机变量,它有 $k$ 种结果,${\displaystyle x_{1}} , {\displaystyle x_{2}} , …, {\displaystyle x_{k}}$,每种结果对应的发生概率是 ${\displaystyle p_{1}}, {\displaystyle p_{2}}, …, {\displaystyle p_{k}}$. ${\displaystyle X}$ 的期望定义如下:
$${\displaystyle \operatorname {E} [X]=x_{1}p_{1}+x_{2}p_{2}+\cdots +x_{k}p_{k}}.$$
因为所有的概率 $p_i$ 相加的和等于1 ( ${\displaystyle p_{1}+p_{2}+\ldots +p_{k}=1}$), 因此,期望可以看作是加权平均,这时候的权重表示的就是概率。
1.4.1 几个常见随机变量的期望
伯努利随机变量的期望是: $E[X]_{Bernoulli} = p$
均匀随机变量的期望是: $E[X]_{Uniform} = \frac{1}{n+1} ( 0 + 1 + 2 + … + n) = \frac{n}{2}$
二项随机变量的期望是:由二项式分布的定义知,随机变量 $X$ 是 $n$ 次伯努利实验中事件 $A$ 发生的次数,且在每次试验中 $A$ 发生的概率为 $p$。因此,可以将二项式分布分解成 $n$ 个相互独立且以 $p$ 为参数的 $(0-1)$ 分布随机变量之和.
所以,$E[X]_{Binomial} = E[X(1) + X(2) + … + X(n)] = np$
1.4.2 期望的特性
如果 $X > 0$, 那么 $E[X] \ge 0$
如果 $a \le X \le b$, 那么$a \le E[X] \le b$
如果 $c$ 是一个常数, 那么 $E[c] = c$